#15

Uso de la información mútua para detectar coapariciones

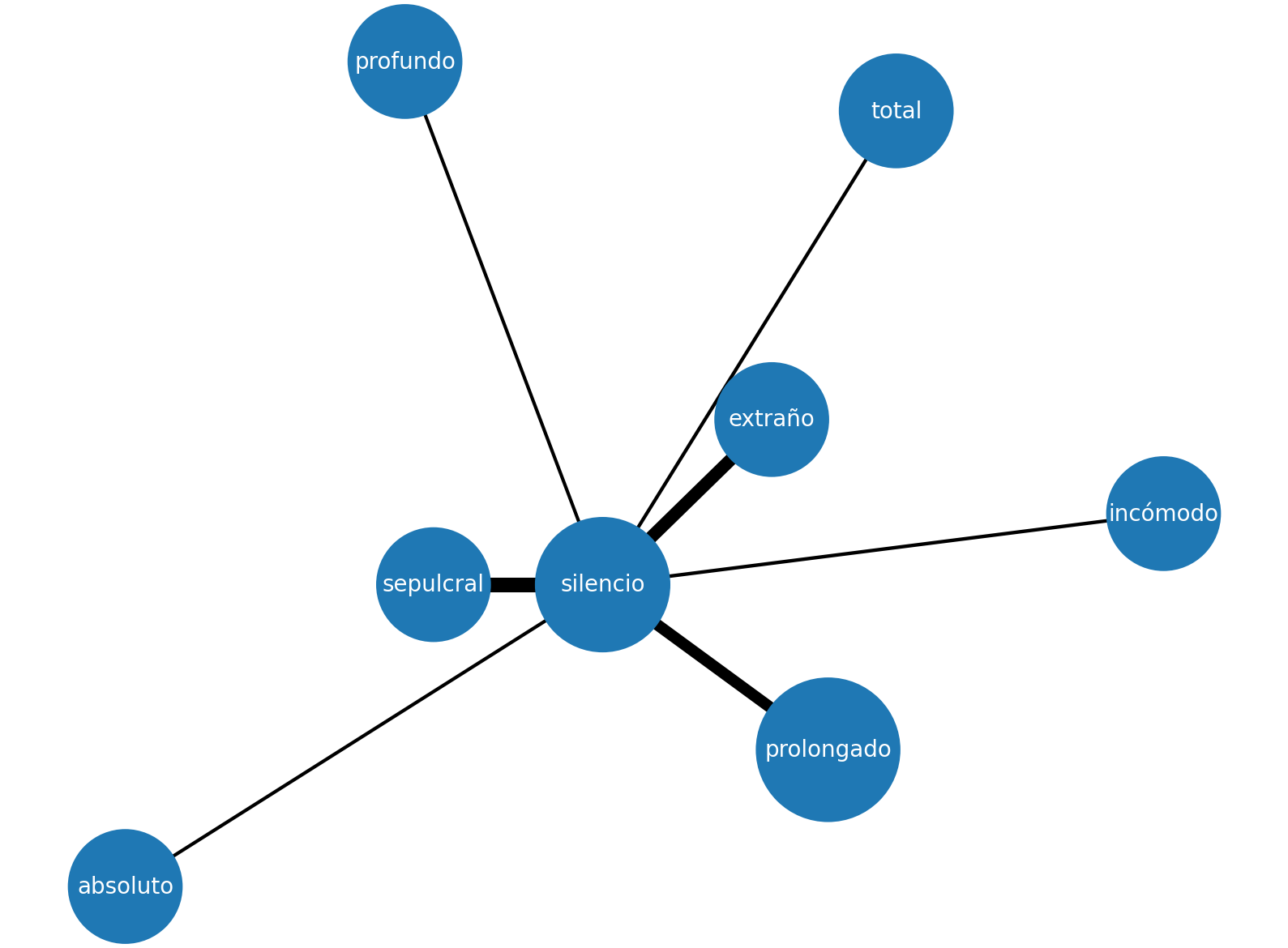
Una coaparición (a menudo denominada también "colocación", de la adaptación del término inglés collocation) es una combinación de palabras restringidas semánticamente que suelen coexistir en un idioma con una frecuencia mayor a lo que cabría esperar del puro azar y que, desde un punto de vista semántico, expresan un significado composicional. Estas combinaciones pueden ocurrir, por ejemplo, entre nombres y adjetivos ("silencio incómodo", "dolor agudo", "viento frío", "mirada penetrante"), entre verbos y adverbios ("correr rápidamente", "esperar pacientemente"), entre nombres y verbos ("tomar medidas", "ganar tiempo") o entre nombres ("una taza de café", "un ramo de flores").

Por otra parte, cuando trabajamos con corpus lingüísticos, una tarea que resulta de interés en investigación es tratar de identificar y estudiar estas coapariciones. Esto nos ayuda a entender mejor cómo funciona realmente un idioma en situaciones auténticas y qué combinaciones de palabras son típicas o frecuentes.

Existen varias maneras de detectar coapariciones en un corpus. Algunas se basan simplemente en contar cuántas veces dos palabras aparecen juntas. Sin embargo, este método tiene limitaciones: por ejemplo, combinaciones frecuentes de palabras como "gato blanco" o "libro nuevo" podrían aparecer con relativa frecuencia simplemente porque ambas palabras son comunes, pero esto no implica necesariamente que sean coapariciones auténticas o significativas en términos semánticos. Otros métodos utilizan cálculos más sofisticados que intentan medir no solo la frecuencia, sino también la fuerza de la asociación entre palabras.

Uno de estos métodos consiste en calcular el punto de información mutua (Pointwise Mutual Information, o simplemente PMI). El PMI mide la asociación entre dos palabras comparando la probabilidad observada de aparición conjunta frente a la probabilidad esperada si fueran independientes. Esta medida de asociación se calcula con la siguiente fórmula:

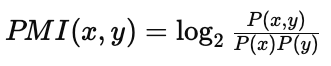
Fórmula del cálculo del PMI

Donde:

P(x,y) es la probabilidad de que las palabras x e y aparezcan juntas.
P(x) es la probabilidad de que la palabra x aparezca individualmente.
P(y) es la probabilidad de que la palabra y aparezca individualmente.

El valor del PMI puede ser positivo o negativo. Un valor positivo indica una asociación entre dos palabras más fuerte que lo que cabría esperar por el azar, mientras que un valor negativo indica una asociación más débil de lo esperado.

Entendiendo los cálculos

Puede ser que hayamos entendido el concepto, pero aún así quedarnos con dudas sobre cómo se hacen los cálculos para obtener el PMI de una posible coaparición, así que vamos a intentar explicar esto. Para empezar, utilizando cálculos relativamente sencillos, la fórmula mostrada anteriormente se podría simplificar, dando lugar a la siguiente:

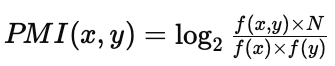
Fórmula del cálculo del PMI usando frecuencias

Donde:

f(x,y) es el número de veces (frecuencia absoluta) que aparecen las palabras x e y juntas en el corpus.
f(x) es el número de veces que aparece la palabra x en el corpus.
f(y) es el número de veces que aparece la palabra y en el corpus.
N es el tamaño del corpus.

NOTA: Si te parece interesante que expliquemos los detalles sobre cómo se hace esta simplificación de la fórmula, pasando de probabilidades a frecuencias, escríbenos y lo haremos en otra entrada.

Pero para poder realizar este cálculo es importante definir qué queremos decir con que dos palabras aparecen juntas en el corpus, ya que tanto en "un silencio incómodo" como en "un silencio anormalmente incómodo", las palabras "silencio" e "incómodo" deberían considerarse como que están "juntas" si estamos intentando hacer el cálculo del PMI para las coapariciones correspondientes a esas dos palabras.

Es por esto que, en la práctica, se debe definir el tamaño de la ventana de contexto, utilizada en cada caso, para determinar si dos palabras aparecen "juntas", y podemos definirlo como el número de palabras a la izquierda y a la derecha de una palabra en la que otra palabra debe estar para que se considere que está junta a la primera más uno (ya que habría que contar también la propia palabra). Para hacer estos cálculos es habitual utilizar un tamaño de ventana de contexto de 5 (2 palabras a la izquierda y 2 a la derecha) 7 (3 palabras a la izquierda y 3 palabras a la derecha) o 9 (4 palabras a la izquierda y 4 palabras a la derecha). De este modo, en la frase "Un silencio anormalmente incómodo llenó la habitación", si trabajamos con una ventana de contexto de 5, las palabras que están en la misma ventana de contexto que "incómodo" serían "silencio", "anormalmente", "llenó" y "la".

Intentemos hacer estos cálculos con un ejemplo concreto de la aplicación de búsquedas del corpus CORPES. Lo que vamos a hacer es buscar las coapariciones de la forma "silencio":

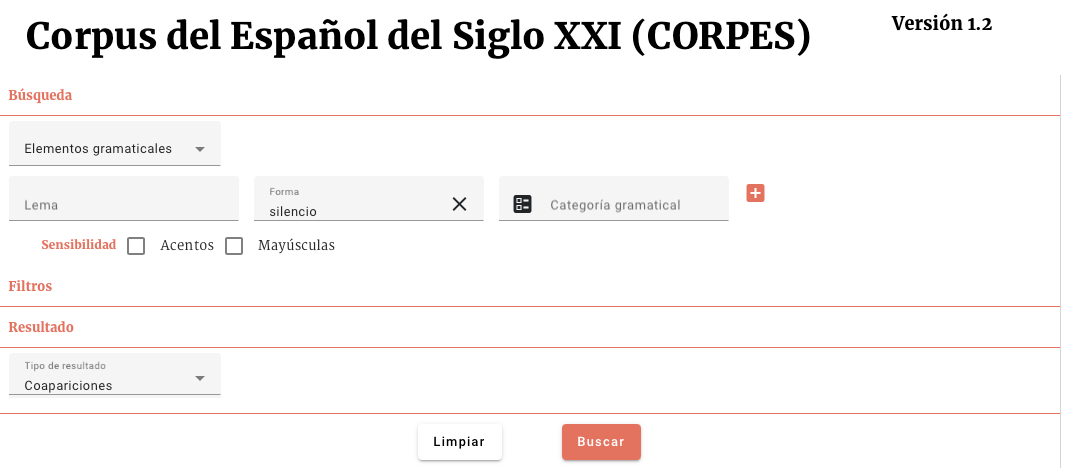
Formulario de búsqueda de CORPES buscando coapariciones de silencio

Y vemos que salen los siguientes resultados:

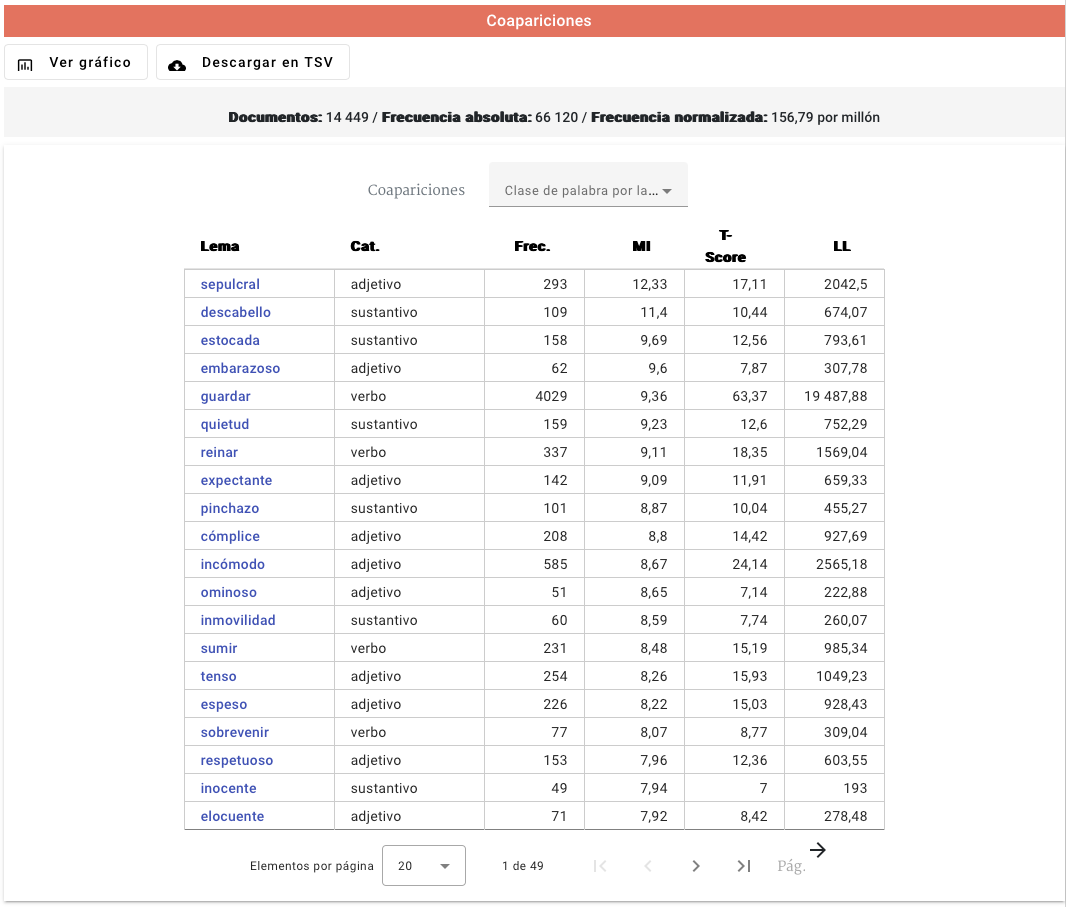
Resultado de coapariciones para silencio

Como se puede apreciar, salen diferentes columnas de estadísticos, pero en este momento nos interesa únicamente la columna MI. Vemos que "sepulcral" es la palabra con un MI más alto para "silencio" y, aunque "guardar" tiene una frecuencia mucho más elevada, su MI es inferior al de "sepulcral". Es decir, que "silencio" y "sepulcral" tienen una fuerza de asociación, según el MI, mucho mayor que "silencio" y "guardar".

Intentemos ahora hacer los cálculos por nosotros/as mismos/as para calcular el PMI de "silencio" y "sepulcral". Tenemos que la frecuencia conjunta de "silencio" y "sepulcral", tal y como se puede observar en la captura anterior es de 293. Es decir, que ya tenemos el valor de f(x,y) en la segunda fórmula explicada anteriormente. f(x) sería la frecuencia de "silencio" en el corpus y f(y) sería la frecuencia de "sepulcral", lo que se puede obtener fácilmente haciendo una búsqueda por separado de ambas palabras, empleando, por ejemplo, el tipo de resultado "Estadísticas".

Si realizamos estas búsquedas podremos comprobar que "silencio" aparece 66.120 veces y "sepulcral" 395 veces. Por lo tanto, ya solo nos falta calcular N, el tamaño del corpus. Ya que en este caso estamos trabajando con búsquedas de elementos gramaticales, lo que debemos hacer es calcular el número de elementos gramaticales que tiene el corpus CORPES. Esto se puede hacer poniendo "*" en el campo forma de la búsqueda (lo que quiere decir, "cualquier forma") del siguiente modo:

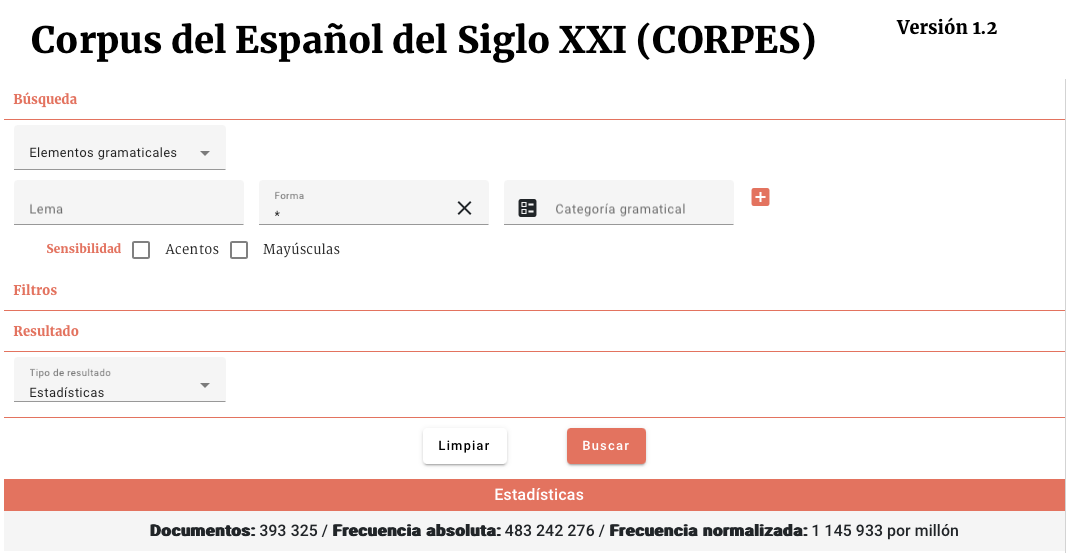
Número de elementos gramaticales del corpus CORPES

Podemos ver que salen 483.242.276 elementos gramaticales en el corpus. Por lo tanto, ya solo nos queda hacer el cálculo:

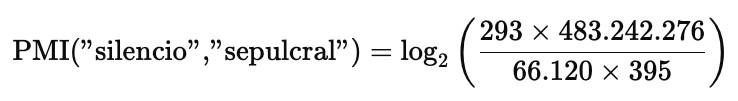
Fórmula del PMI para "silencio" y "sepulcral"

Si hacemos las cuentas nos sale un valor para el PMI de "silencio" y "sepulcral" de 12,40. De acuerdo, no nos ha salido el 12,33 que muestra la aplicación, pero sí un número muy aproximado. Esto puede deberse a que en el corpus se esté haciendo algún ajuste que desconozcamos, seguramente relacionado con el cálculo total del número de elementos gramaticales del corpus, pero en cualquier caso, esto no invalida la explicación.

Eliminando valores negativos

El cálculo del PMI puede dar valores negativos, a menudo difíciles de interpretar, por lo que, en la práctica, se suele utilizar el PPMI (Positive Pointwise Mutual Information), que es el que se utiliza en CORPES, ya que se puede comprobar que no aparecen nunca valores negativos. Por lo tanto, lo que hace el PPMI es simplemente poner a cero los resultados negativos del PMI. Matemáticamente esto se representa así:

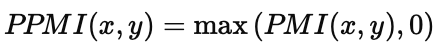
Fórmula del cálculo del PPMI

Interpretar el valor del PPMI es sencillo: cuanto mayor sea el número obtenido, más fuerte será la relación entre las palabras. Un valor alto indica una coaparición fuerte, mientras que un valor cercano a cero significa que probablemente la aparición conjunta de esas palabras sea casual o poco significativa.

Por otra parte, aunque no existe una regla universal que indique exactamente a partir de qué valor un PPMI es alto, ya que esto depende del tamaño y tipo del corpus, y del análisis específico que se esté realizando, de manera orientativa se suele considerar que:

Un PPMI cercano a 0 indica que la asociación entre las palabras es prácticamente inexistente o casual.
Valores entre 1 y 3 suelen reflejar una asociación moderada.
Valores mayores de 3 ya sugieren una asociación fuerte, con alta probabilidad de que exista una coaparición auténtica.

En investigaciones lingüísticas o análisis prácticos con corpus grandes, se suelen utilizar umbrales en torno a 2 o más como criterio inicial para identificar combinaciones significativas.

Inconvenientes del empleo de la información mutua

Aunque el cálculo de la información mutua, en cualquier de sus variantes (PMI/PPMI), constituye una herramienta eficaz para identificar coapariciones, presenta también algunos inconvenientes:

Sesgo hacia palabras poco frecuentes: La información mutua tiende a sobrevalorar asociaciones entre palabras poco frecuentes. Esto ocurre porque cuando las frecuencias son bajas, pequeños aumentos en la coaparición pueden producir valores artificialmente altos, lo que podría llevar a conclusiones erróneas.
Ausencia de una escala claramente interpretable: Aunque sabemos que valores altos indican relaciones fuertes, no podemos definir una escala absoluta universal. Los cálculos de la información mutua dependen del tamaño del corpus y su composición, por lo que un mismo valor puede no indicar la misma fuerza de asociación en corpus diferentes.
Sensibilidad al tamaño del corpus: El cálculo de la información mútua es sensible al tamaño del corpus y, en corpus pequeños, se pueden producir muchas asociaciones espurias con valores elevados, lo que los hacen más indicados para corpus grandes.

Conclusiones

En este artículo hemos explicado qué son las coapariciones y cómo usar el cálculo del PMI para obtenerlas. También hemos visto tanto su utilidad como sus debilidades y confiamos en que este artículo permita a estudiantes y lingüistas a entender e interpretar mejor los resultados en el intento de descubrir coapariciones relevantes y auténticas de un idioma.